저번 포스팅에 이어서, Ch.5 Model Validation and Diagnotics을 마무리하고자 한다.
https://taesungha.tistory.com/2
Ch.5 Model Validation and Diagnotics-(1)
Ch.5전까지 우리는 data를 linear regression model로 fitting하고, 이 model의 prediction power가 어떤지, 또는 회귀계수 전체 또는 일부에 대한 가설검정, 또는 회귀계수에 대한 confidence interval을 구하는..
taesungha.tistory.com
https://taesungha.tistory.com/5
Ch.5 Model Validation and Diagnotics-(2)
전 포스팅에 이어 목차 3의 Generalized Least Squares Regression에 대해 포스팅하겠다. https://taesungha.tistory.com/2 Ch.5 Model Validation and Diagnotics-(1) Ch.5전까지 우리는 data를 linear regressio..
taesungha.tistory.com
이번 포스팅은 Ch 5의 목차 4번째, Lack of Fit Test를 다룬다.
Ch 5는 챕터의 제목에서도 알 수 있듯이, 우리가 사용하려는 Multiple Linear Regression Model(이하 MLRM)의 가정을 확인해보고, 맞지 않으면 어떤 행동을 취해야하는지에 대해서 논의하고 있다. 아래는 Ch.5 4개의 목차다.
- Leverage and Influential Observation
- Scaled Residual
- Generalized Least Squares Regression
- Lack of Fit Test
1부터 3까지의 story를 간단히 풀어내자면, 일단 우리가 사용하는 모델에서 영향을 많이 주는 observation이 무엇인지(Leverage and Influential Observation) 확인하는 방법을 공부했다. 만약, 특정 observation이 회귀직선에 너무나도 큰 영향을 끼치는데, EDA 관점에서 확인했을 때 이상치에 해당한다면, 우리는 그 데이터를 제거하거나 대체할 것이다. 두 번째로 우리는 MLRM이 깔고 있는 기본적인 가정들(Normality Assumption, homoskedasticity, 독립성)을 확인하는 방법으로 Scaled Residual을 공부하였다. 구체적인 예로는 externally Studentized Residual의 분포를 통해 t분포를 따르는지 확인하여 위의 가정을 만족하는지에 대해 알 수 있었다. 세 번째 Generalized Least Squares Regression(이하 GLS)은 위 가정을 따르지 않을 때, 더 구체적으로는 모든 가정은 똑같은데, 만약 MLRM의 분산이 \(\sigma^2V\)을 따를 때, 어떻게 대처해야하는지(GLS를 구한다), 그리고 그 GLS가 가장 최선의 방법인지(Gauss-Markov Theorem)에 대해 공부하였다.
목차 4 Lack of Fit Test는 좀 더 model에 대한 근본적인(?) 질문을 하고자 한다. 즉, 우리의 model이 정말 MLRM이 맞느냐? 선형적이냐?라는 것이다.
이러한 우리의 물음은, Hypothesis 관점으로 볼 때 다음과 같이 표현이 가능하다.
\[ y=f(x_1,x2,\,...\,,x_p) +\,\varepsilon ,\quad\varepsilon \sim N(0,\sigma ^2)\]일 때,
\(H_0:\,y=f(x_1,x2,\,...\,,x_p) = \beta _0+\beta _1x_1+...+\beta _px_p\) versus \(H_1:\,not\,H_0\)
그러면, 이 가설을 어떻게 검정할 것인가?
먼저, under H0일 때(귀무가설이 참이라고 했을 때) 다음과 같이 표현할 수 있다.
\[ E(y)=\beta _0+\beta _1x_1+...+\beta _px_p \]
여기서, 우리는 H0가 참이라고 가정했으므로, 우변에 대해서 저렇게 쓰여지는 건 자연스럽게 이해할 수 있다.
문제는, 물론 MLRM일 때 \(E(y))\가 우변과 같겠지만, 우리는 정말 MLRM이 맞는지 보고 싶기 때문에 좌변의 \(E(y)\)를 다른 방법으로 표현해서 좌변과 우변의 discrepancy가 어느 정도인지 평가하고 싶은 것이다. 만약 discrepancy가 작다면, 우리는 가설을 기각할 수 없을 것이다.
' 좌변의 \(E(y)\)를 다른 방법으로 표현'하기 위해 우리는 \(i\)번째 predictor value인 \(x_{1,i},x_{2,i},...,x_{p,i}\)를 고정하고 이에 해당하는 \(y_i\)를 반복측정해준다. 이런 방법으로, \(n\)개의 관측치에 대해 각각 수행하면 우리는 아래와 같은 수식을 얻는다.

우리는 vector form일 때 더 간단해지고, test를 하기 쉬워지기 때문에 위 식을 vector form으로 다시 표현해보겠다. 이는 아래와 같다.

우리는 predictor는 고정해두고 response 변수만 여러 번 측정했기 때문에, 위와 같은 vector form을 얻을 수 있다. 이를 좀 더 축약해보면 아래와 같다.

이제 vector form까지 얻었으니, LSE를 구하는건 문제도 아니다. 다만 여기서 추가적으로 알아두면 좋은 점은, \(y_F\)의 LSE가 weighted LS로 표현이 가능하다는 것이다. 해당 derivation은 아래와 같다.

\(Y_F\)의 LSE도 알았고, 이제는 SSE를 구하고, decompose 해보자.

보는 바와 같이 우변의 3번째 term은 0이 되어 없어진다. SSPE와 SSLF의 의미를 살펴보자.
SSPE = \(\sum _i \sum _j(y_{ij}-\bar y_i)^2\) 로 표현된다. SSPE는 Sum of Square Pure Error인데 식을 보면, model이 어떻게 fitted 되던 간에 상관없이 SSPE는 존재한다는 것을 알 수 있다. 이름처럼 순수한 에러에 해당한다고 볼 수 있다.
SSLF= \(\sum _i \sum _j(\bar y_i-\hat y_i)^2\)로 표현된다.SSLF는 Sum of Square Lack of FIt인데, 식에서는 model이 data를 잘 맞추는 식으로 fitted된다면, 충분히 값이 줄어들 수 있다. 여기서 우리는 SSLF의 값을 기준으로 \(H_0\)을 검정하고자 한다. 즉, SSLF가 낮으면 \(H_0\)을 기각한다. 다만, SSLF의 식을 그대로 가져가서 검정할 수는 없고, 우리가 아는 카이검정제곱과 F분포로 통계량을 만들어 검정해야한다.
일단, \(\bar Y_F\)와 \(\hat Y_F\)를 다음과 같이 정의해보자.

또한, \(X_P\), \(X_F\)를 다음과 같이 써보자.


그리고, \(C(X_P)\)로의 projection인 \(\Pi_P\)을 정의해주고, \(Y_F\)를 , \(C(X_P)\)로의 projection하면 다음과 같아진다. 즉, \(\bar y_F\)가 된다.

이를, SSPE에 적용시켜보자. 그러면 다음과 같은 식을 얻을 수 있다.

한편, \(\hat Y_F\)은 아래처럼 \(\Pi_F Y_F\)가 된다.

이제, SSLF에 적용시켜보자.

여기에서, \((\Pi_P-\Pi_F)^2\) 가 \(\Pi_P-\Pi_F\)가 되는 것은 선형대수적인 이해가 필요한데, 이 포스팅에 모든 것을 다 설명하기에는 부족하므로, 차후 Linear Algebra 카테고리에 개념을 정리하도록 하겠다.
이제, quadratic form으로 변형된 SSLF,SSPE에 대해 다음과 같은 사실을 증명한다.
(a)

이는, \(SSLF/\sigma^2\)가 카이제곱(n-p-1)을 따른다는 사실을 증명한 것이다. 이는, \(Y_F\)가 N(\(X\beta,sigma^2I)\)를 따른다는 것에서부터 비롯되는 정규분포 관련 Theorem을 확인하면 알 수 있다.
(b)

(b)에 대한 증명도 위와 같다.
(c)
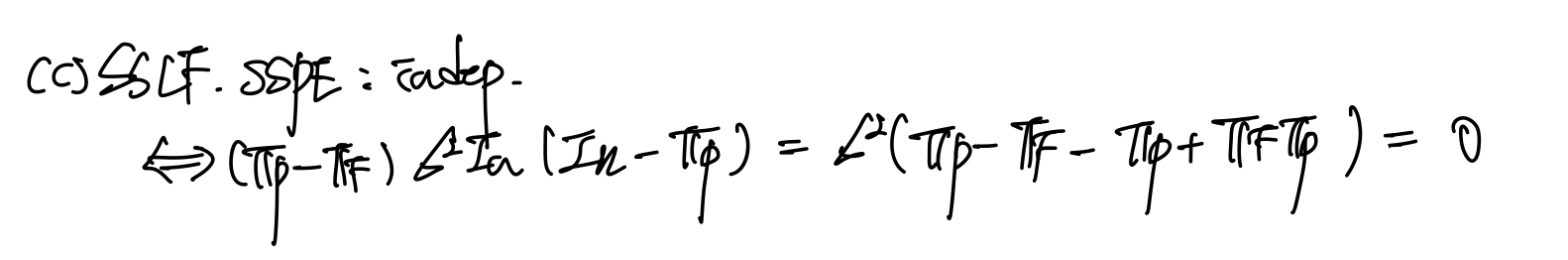
SSLF와 SSPE가 모두 정규분포 행렬 곱 사이에 껴있는(?) 형태이므로, SSLF와 SSPE의 사이의 행렬 2개의 곱이 0이면 independent하다는 사실에서, SSLF와 SSPE가 독립이라는 것을 알 수 있는 증명이다. 위에 대한 증명들이 이해가 안될 수 있는데, 차후 관련된 Theorem들을 포스팅으로 정리해보겠다.
이제, (a),(b),(c)를 통해, 우리는 가설검정이 가능해졌다. 즉, \(H_0\)가 참이라는 가정 하에(MLRM is True),
\( F=\frac{SSLF/(n-p-1)}{SSPE/(N-n)}\)이 \(F(n-p-1,N-n)\)을 따르기 때문이다. 여기서, F분포가 SSLF에 대한 증가함수라는 사실도 가설검정할 수 있는 통계량이라는 근거가 된다.
이로서, Ch.5 Model Validation and Diagnotics를 마친다.
'Statistics > Regression Analysis' 카테고리의 다른 글
| Ch.4 Constrained Least Square Estimation - (1) (0) | 2022.06.29 |
|---|---|
| Ch.7 Biased Regression - (1) (0) | 2022.06.25 |
| Ch.6 Non-full-rank Model-(1) (0) | 2022.06.22 |
| Ch.5 Model Validation and Diagnotics-(2) (0) | 2022.06.20 |
| Ch.5 Model Validation and Diagnotics-(1) (0) | 2022.06.20 |



댓글